Linear Algebra Primer

Vectors and matrices

Vectors and matrices are just collections of ordered numbers that represent something: movements in space, scaling factors, pixel brightness, etc.

Vectors

1. A column vector

2. A row vector , $T$ denotes the transpose operation

Matrix

A matrix , if , we say that A is square

Grayscale images have one number per pixel, so they are stored as an matrix. Color images have 3 numbers per pixel - red, green, and blue brightnesses, so they are stored as an matrix.

Basic Matrix Operations

1. Addition

2. Scaling

3. Inner product

4. Multiplication

5. Powers

;

6. Transpose

7. Determinant

returns a scalar for ,

• means $A$ is singular

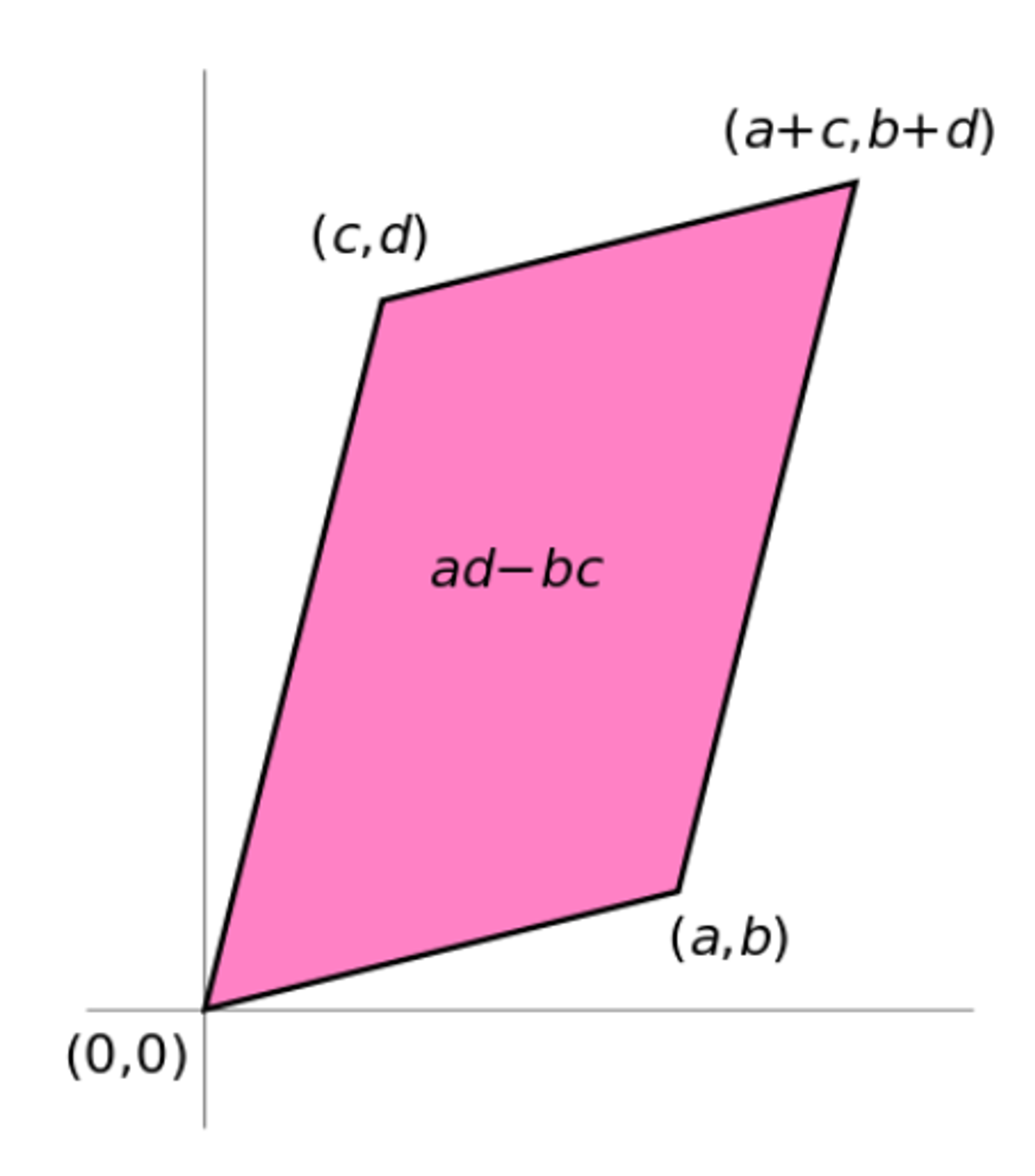
8. Trace

= sum of diagonal elements

Special Matrices

1. Identity Matrix

2. Diagonal Matrix

3. Symmetric Matrix

4. Skew-symmetric Matrix

Transformation Matrices

1. Translation

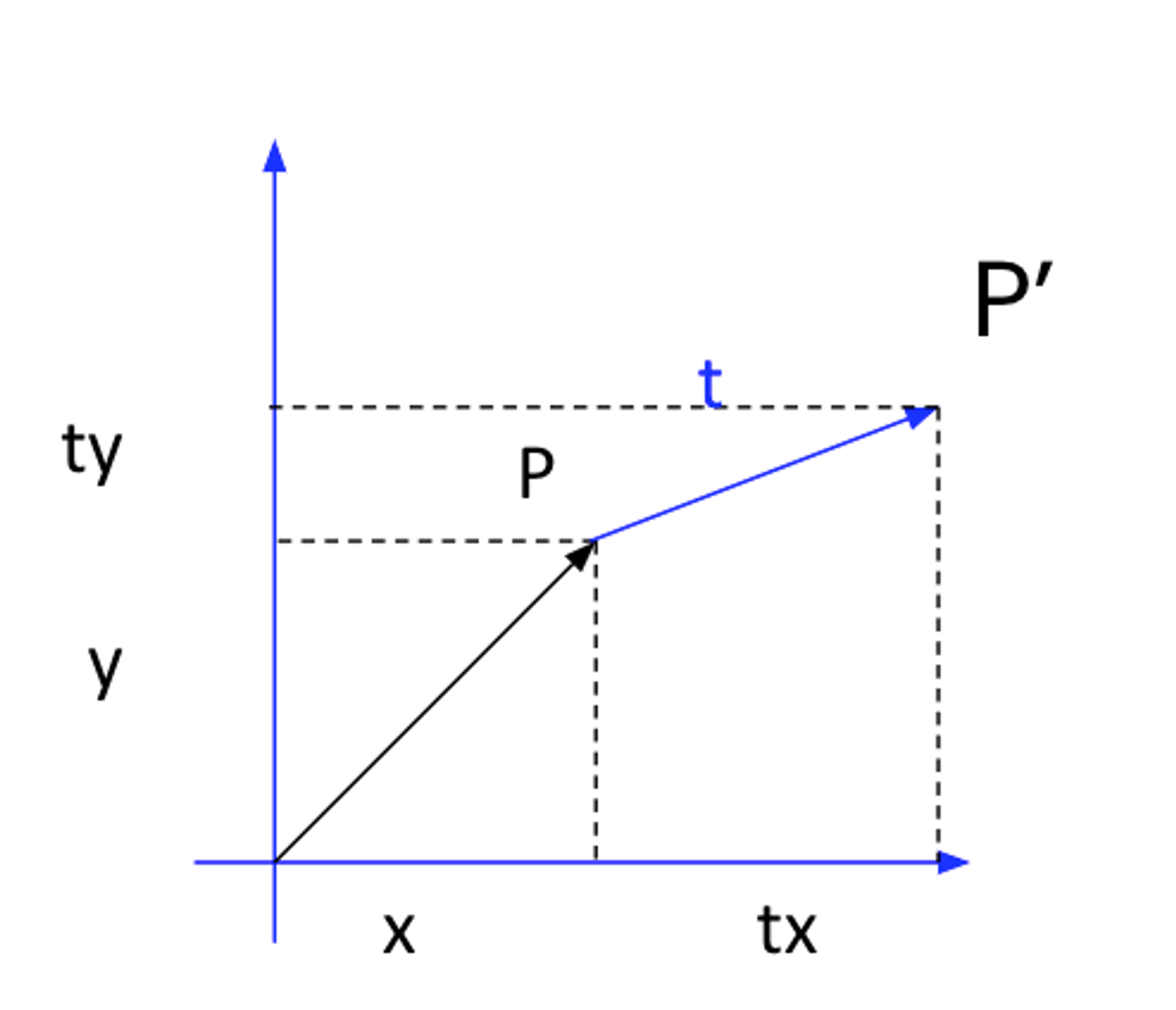
2. Scaling

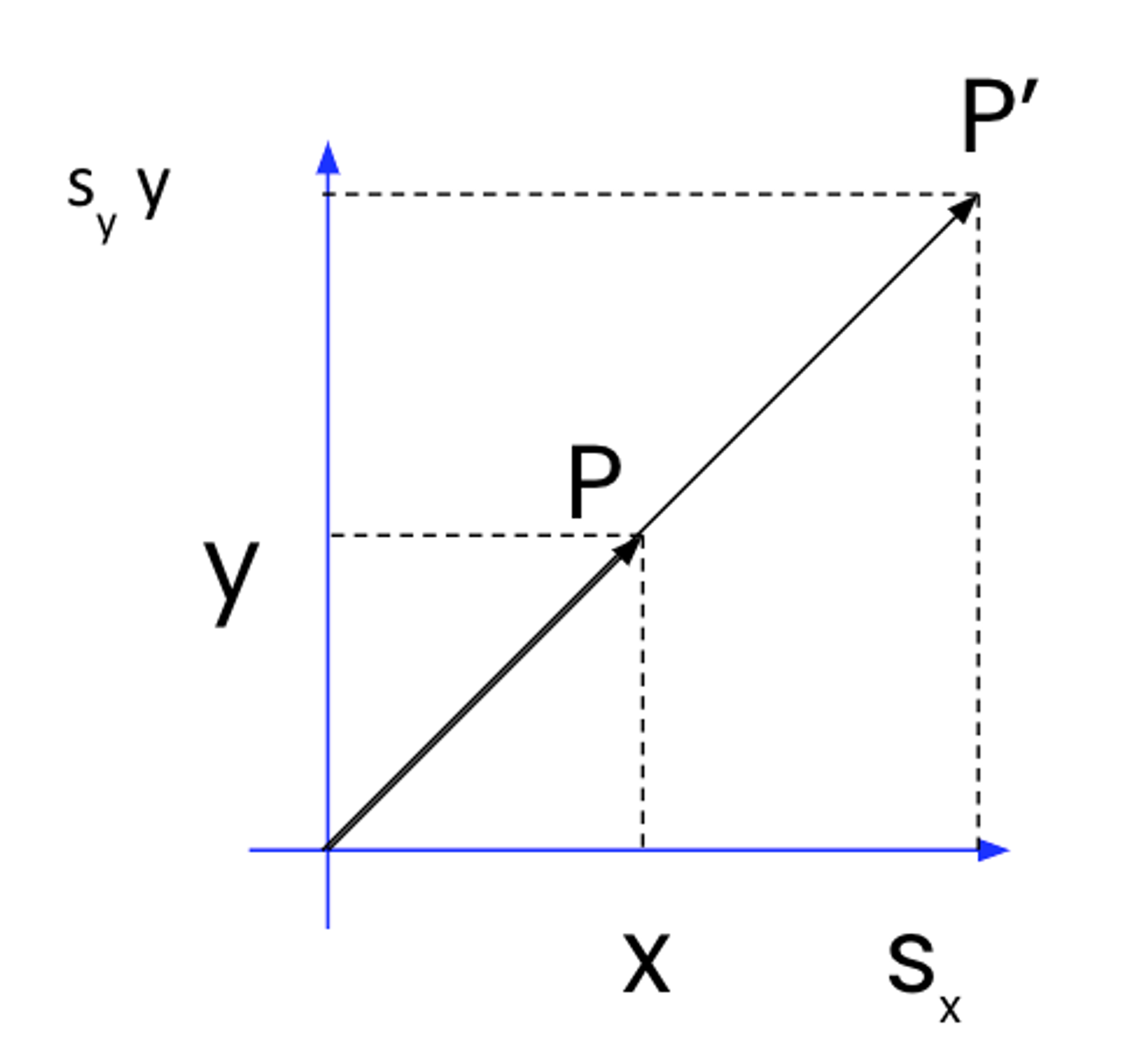
3. Translation & Scaling

4. Rotation

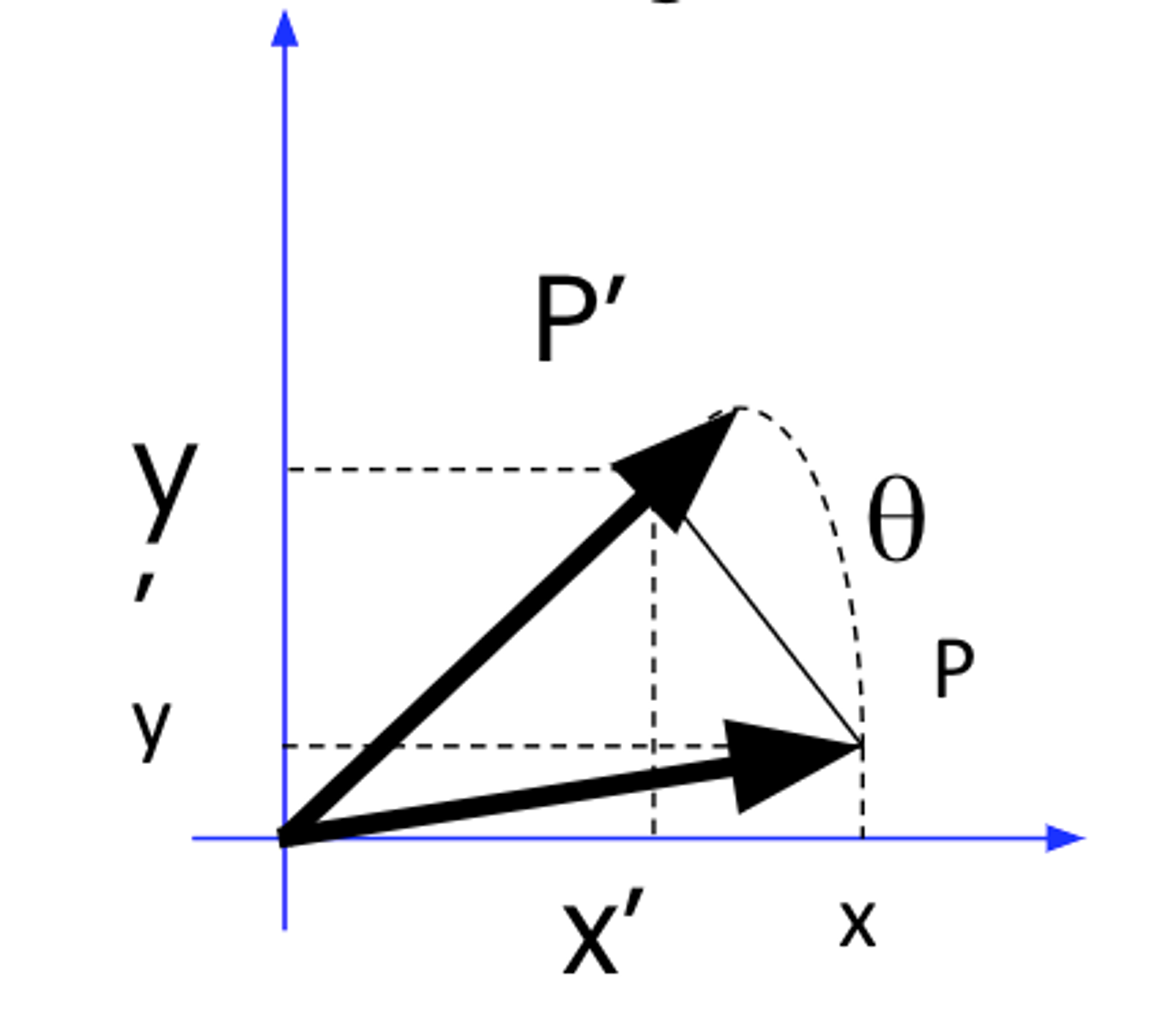
5. Rotation & Translation & Scaling

Matrix Inverse

e.g.

Matrix Rank

The number of linearly independent columns, e.g.

has rank 2: the first two columns are linearly independent, but the third is a linear of the first two(the first column minus the second).

Singular Value Decomposition(SVD)

• $U$ and $R$ are always rotation matrices
• is a diagonal matrix which sorts from high to low